Verschil tussen gemiddeld en mediaan
 Share
Share
 Centrale tendens impliceert de neiging van de datapunten om zich te centreren rond zijn centrale of middelste waarde. De twee meest gebruikte maatstaven voor centrale tendentie zijn gemiddelde en mediaan. Gemiddelde wordt gedefinieerd als de 'centrale' waarde van de gegeven set gegevens, terwijl mediaan- is de 'middelste' waarde in de gegeven reeks gegevens.
Centrale tendens impliceert de neiging van de datapunten om zich te centreren rond zijn centrale of middelste waarde. De twee meest gebruikte maatstaven voor centrale tendentie zijn gemiddelde en mediaan. Gemiddelde wordt gedefinieerd als de 'centrale' waarde van de gegeven set gegevens, terwijl mediaan- is de 'middelste' waarde in de gegeven reeks gegevens.
Een ideale maat voor centrale tendens is er een die duidelijk gedefinieerd, gemakkelijk te begrijpen, eenvoudigweg berekenbaar is. Het moet gebaseerd zijn op alle waarnemingen en het minst worden beïnvloed door extreme waarnemingen die aanwezig zijn in de dataset.
Mensen stellen deze twee maten vaak tegenover elkaar, maar het feit is dat ze anders zijn. Dit artikel belicht specifiek de fundamentele verschillen tussen gemiddelde en mediaan. Even kijken.
Inhoud: gemiddeld versus mediaan
Vergelijkingstabel
| Basis voor vergelijking | Gemiddelde | Mediaan |
|---|---|---|
| Betekenis | Gemiddelde verwijst naar het eenvoudige gemiddelde van de gegeven reeks waarden of grootheden. | Mediaan wordt gedefinieerd als het middelste getal in een geordende zoeklijst. |
| Wat is het? | Het is een rekenkundig gemiddelde. | Het is positioneel gemiddelde. |
| vertegenwoordigt | Zwaartepunt van de gegevensverzameling | Zwaartepunt van de gegevensverzameling Halverwege de gegevensverzameling |
| toepasselijkheid | Normale verdeling | Scheve verdeling |
| uitschieters | Gemiddelde is gevoelig voor uitschieters. | Mediaan is niet gevoelig voor uitschieters. |
| Berekening | Het gemiddelde wordt berekend door alle waarnemingen bij elkaar op te tellen en vervolgens de verkregen waarde te delen door het aantal waarnemingen. | Voor het berekenen van de mediaan wordt de gegevensset in oplopende of aflopende volgorde gerangschikt, waarna de waarde die precies in het midden van de nieuwe gegevensset valt, de mediaan is. |
Definitie van Mean
Het gemiddelde is de veelgebruikte maat voor de centrale tendens, die wordt gedefinieerd als het gemiddelde van de reeks waarden. Het vertegenwoordigt het model en de meest voorkomende waarde van het gegeven waardenbereik. Het kan worden berekend, zowel in discrete als doorlopende reeksen.
Het gemiddelde is gelijk aan de som van alle waarnemingen gedeeld door het aantal waarnemingen in de gegevensset. Als de waarde die wordt aangenomen door een variabele gelijk is, zal het gemiddelde ook hetzelfde zijn. Het gemiddelde kan uit twee typen zijn, het steekproefgemiddelde (x̅) en het populatiegemiddelde (μ). Het kan worden berekend met de gegeven formule:
- Rekenkundig gemiddelde:
 waarbij Σ = Griekse letter sigma, duidt op 'som van ...'
waarbij Σ = Griekse letter sigma, duidt op 'som van ...'
n = aantal waarden - Voor Discrete Series:
 waar, f = frequentie
waar, f = frequentie - Voor continue servies:
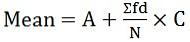 waarbij d = (X-A) / C
waarbij d = (X-A) / C
A = Aangenomen gemiddelde
C = gemeenschappelijke deler
Definitie van mediaan
De mediaan is een andere belangrijke maat voor de centrale tendens, die wordt gebruikt om de waarde in twee gelijke delen te verdelen, d.w.z. grotere helft van het monster, populatie of waarschijnlijkheidsverdeling van de onderste helft. Het is de middelste waarde, die wordt verkregen wanneer de waarnemingen in een specifieke volgorde worden gesorteerd, in oplopende of aflopende volgorde.
Voor de berekening van de mediaan, eerst en vooral, rangschik de waarnemingen in de laagste tot de hoogste of hoogste tot de laagste, en pas dan de juiste formule toe, volgens de onderstaande voorwaarden:
- Als het aantal waarnemingen oneven is:
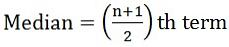 waarbij n = aantal waarnemingen
waarbij n = aantal waarnemingen - Als het aantal waarnemingen is zelfs:
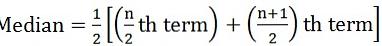
- Voor continue series:
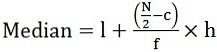 waar, l = ondergrens van de mediane klasse
waar, l = ondergrens van de mediane klasse
c = cumulatieve frequentie van de voorgaande mediane klasse
f = frequentie van de mediane klasse
h = klasse breedte
Belangrijkste verschillen tussen gemiddeld en mediaan
De significante verschillen tussen gemiddelde en mediaan zijn te vinden in het artikel hieronder:
- In statistieken wordt een gemiddelde gedefinieerd als het eenvoudige gemiddelde van de gegeven reeks waarden of grootheden. De mediaan is het middelste cijfer in een geordende lijst met waarden.
- Terwijl het gemiddelde het rekenkundig gemiddelde is, is de mediaan het positiegemiddelde, in wezen bepaalt de positie van de gegevensset de waarde van de mediaan.
- Het gemiddelde schetst het zwaartepunt van de gegevensverzameling terwijl de mediaan de middelste waarde van de gegevensset markeert.
- Het gemiddelde is geschikt voor normaal verdeelde gegevens. Aan de andere kant is de mediaan het beste wanneer de gegevensverdeling scheef is.
- Het gemiddelde wordt sterk beïnvloed door de extreme waarde die niet het geval is bij een mediaan.
- Het gemiddelde wordt berekend door alle waarnemingen bij elkaar op te tellen en vervolgens de verkregen waarde te delen door het aantal waarnemingen; het resultaat is gemeen. In tegenstelling tot de mediaan is de gegevensverzameling gerangschikt in oplopende of aflopende volgorde, waarna de waarde die in het exacte midden van de nieuwe gegevensset valt, de mediaan is.
Voorbeeld
Zoek het gemiddelde en de mediaan van de gegeven reeks gegevens:
58, 26, 65, 34, 78, 44, 96
Oplossing: om het gemiddelde te berekenen, moet u de som van de waarnemingen verdelen met het aantal waarnemingen,

 Gemiddeld = 57.28
Gemiddeld = 57.28
Om de mediaan te berekenen, rangschikt u eerst de reeks in een reeks, d.w.z. van het laagste naar het hoogste,
26, 34, 44, 58, 65, 78, 96
 waarbij n = aantal waarnemingen
waarbij n = aantal waarnemingen
Conclusie
Na het bekijken van de bovenstaande punten kunnen we zeggen dat deze twee wiskundige concepten anders zijn. Het rekenkundig gemiddelde of gemiddelde wordt beschouwd als de beste maat voor de centrale tendens, omdat het alle kenmerken van een ideale maat bevat, maar het heeft als nadeel dat de fluctuaties van de bemonstering het gemiddelde beïnvloeden..
Op dezelfde manier is de mediaan ook ondubbelzinnig gedefinieerd en gemakkelijk te begrijpen en te berekenen, en het beste van deze maatregel is dat hij niet wordt beïnvloed door fluctuaties in steekproefsgewijze metingen, maar het enige nadeel van de mediaan is dat deze niet gebaseerd is op alle observaties. Voor open-endclassificatie heeft de mediaan normaliter de voorkeur boven het gemiddelde.
 waarbij Σ = Griekse letter sigma, duidt op 'som van ...'
waarbij Σ = Griekse letter sigma, duidt op 'som van ...' waar, f = frequentie
waar, f = frequentie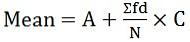 waarbij d = (X-A) / C
waarbij d = (X-A) / C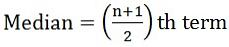 waarbij n = aantal waarnemingen
waarbij n = aantal waarnemingen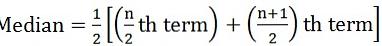
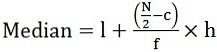 waar, l = ondergrens van de mediane klasse
waar, l = ondergrens van de mediane klasse Mediaan = 4th termijn = 58
Mediaan = 4th termijn = 58