Hoe de asymptoten van een hyperbol te vinden
 Share
Share
Hyperbool
De hyperbool is een kegelsnede. De term hyperbool verwijst naar de twee niet-verbonden curven die in de figuur worden getoond.
Als de hoofdassen samenvallen met de cartesiaanse assen, is de algemene vergelijking van hyperbool van de vorm:

Deze hyperbolas zijn symmetrisch rond de y-as en staan bekend als de hyperbool op de y-as. De hyperbool symmetrisch rond x-as (of x-as hyperbool) wordt gegeven door de vergelijking,
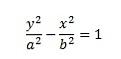 Hoe de asymptoten van een hyperbool te vinden
Hoe de asymptoten van een hyperbool te vinden
Om de asymptoten van een hyperbool te vinden, gebruikt u een eenvoudige manipulatie van de vergelijking van de parabool.
ik. Breng eerst de vergelijking van de parabool naar boven gegeven vorm
Als de parabool wordt gegeven zoals mx2+ny2=l, door te definiëren
een= √ (l/m) en b= √ (-l/n) waar l<0
(Deze stap is niet nodig als de vergelijking standaard wordt gegeven vanaf.

ii. Vervang dan de rechterkant van de vergelijking door nul.

iii. Factoriseer de vergelijking en neem oplossingen

Daarom zijn de oplossingen ,

Vergelijkingen van de asymptoten zijn

Vergelijkingen van de asymptoten voor de hyperbool op de x-as kunnen ook op dezelfde manier worden verkregen.
Zoek de asymptoten van een hyperbool - Voorbeeld 1
Beschouw de hyperbool gegeven door de vergelijking x2/ 4-y2/ 9 = 1. Zoek de vergelijkingen van de asymptoten.

Herschrijf de vergelijking en volg de bovenstaande procedure.
X2/ 4-y2/ 9 = x2/ 22 -Y2/ 32 = 1
Door de rechterkant te vervangen door nul, wordt de vergelijking x2/ 22 -Y2/ 32 = 0.
Factorizing and taking solution of the equation geven,
(X / y-2/3) (x / 2 + y / 3) = 0
Vergelijkingen van de asymptoten zijn,
3x-2y = 0 en 3x + 2y = 0
Zoek de asymptoten van een hyperbool - Voorbeeld 2
- Vergelijking van een parabool wordt gegeven als -4x² + y² = 4

Deze hyperbool is een hyperbool met een X-as.
Herschikken van de voorwaarden van de hyperbool in de standaard van geeft
-4x2+ Y2= 4 => y2/ 22 -X2/ 12 = 1
Factorizing the equation levert het volgende op
(Y / 2-x) (y / 2 + x) = 0
Daarom zijn de oplossingen y-2x = 0 en y + 2x = 0.
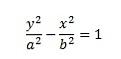 Hoe de asymptoten van een hyperbool te vinden
Hoe de asymptoten van een hyperbool te vinden 