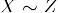Verschil tussen gelijk en gelijkwaardig
 Share
Share
Belangrijkste verschil - Equal vs. Equivalent
Gelijk en gelijkwaardig zijn termen die vaak in de wiskunde worden gebruikt. De grootste verschil tussen gelijk en equivalent is dat de term gelijk verwijst naar dingen die in alle opzichten vergelijkbaar zijn, terwijl de term equivalent verwijst naar zaken die op een bepaald aspect vergelijkbaar zijn. Merk op dat in de verzameltheorie, de woorden "gelijk" en "equivalent" hebben specifieke betekenissen, zoals we hieronder zullen zien.
Wat betekent Gelijke betekenis
Over het algemeen zijn twee dingen gelijk als ze in alle opzichten vergelijkbaar zijn.
In het geval van set-theorie zijn twee sets gelijk als ze allebei dezelfde elementen bevatten. De bestellen waarin ze voorkomen in een set maakt niet uit. Bijvoorbeeld, stel dat
 en
en
 dan,
dan,
de set  is gelijk aan de set
is gelijk aan de set  .
.
Wat betekent equivalent
Van twee dingen kan worden gezegd dat ze gelijkwaardig zijn als ze vergelijkbaar zijn in een bepaalde situatie. Daarom, of twee entiteiten zijn gelijkwaardig grotendeels ligt eraan op de voorwaarde die we gebruiken om hun gelijkwaardigheid te beschrijven. De nummers 2 en 7 zijn bijvoorbeeld equivalent in de zin dat ze beide priemgetallen zijn. Echter, als de voorwaarde waarin we geïnteresseerd zijn er achter komt of getallen even zijn, dan zijn in deze zin 2 en 7 dat wel niet gelijkwaardig. We gebruiken de symbolen  of
of  om dat aan te geven
om dat aan te geven  en
en  zijn gelijkwaardig.
zijn gelijkwaardig.
Als een criterium eenmaal is gedefinieerd, voldoen de equivalente dingen aan de equivalentie relaties:
- reflexiviteit:
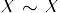
- Symmetrie: Als
 , dan
, dan 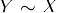
- transitiviteit: Als
 en
en 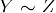 , dan
, dan 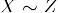
In de set-theorie zijn twee sets gelijkwaardig als ze hetzelfde aantal elementen hebben. De elementen zelf hoeven ook niet hetzelfde te zijn, enkel en alleen het aantal elementen moet hetzelfde zijn. Bijvoorbeeld, stel dat
 en
en
 dan,
dan,
de sets  en
en  zijn gelijkwaardig.
zijn gelijkwaardig.

Symbolen voor het uitdrukken van gelijkheid en gelijkwaardigheid
Verschil tussen gelijk en gelijkwaardig
Algemene betekenis
Wanneer twee dingen zijn Gelijk, ze zijn vergelijkbaar in alle aspecten.
Wanneer dingen zijn gelijkwaardig, ze zijn vergelijkbaar in een bepaald aspect.
In de steltheorie
Wanneer twee sets zijn Gelijk, ze bevatten dezelfde elementen.
Wanneer twee sets zijn gelijkwaardig, ze bevatten hetzelfde aantal elementen.
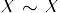
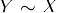
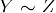 , dan
, dan