Verschil tussen Laplace en Fourier-transformaties

Laplace versus Fourier-transformaties
 

Zowel Laplace-transformatie als Fourier-transformatie zijn integrale transformaties, die meestal worden gebruikt als wiskundige methoden om mathematisch gemodelleerde fysieke systemen op te lossen. Het proces is eenvoudig. Een complex wiskundig model wordt omgezet in een eenvoudiger, oplosbaar model met behulp van een integrale transformatie. Zodra het eenvoudiger model is opgelost, wordt de inverse integrale transformatie toegepast, die de oplossing zou bieden voor het oorspronkelijke model.

Omdat de meeste van de fysieke systemen bijvoorbeeld differentiaalvergelijkingen opleveren, kunnen ze worden omgezet in algebraïsche vergelijkingen of in relatief eenvoudig oplosbare differentiaalvergelijkingen in lagere graden met behulp van een integrale transformatie. Dan wordt het oplossen van het probleem eenvoudiger.

Wat is de Laplace-transformatie?

Gegeven een functie f (t) van een echte variabele t, zijn Laplace-transformatie wordt gedefinieerd door de integraal 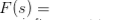(wanneer het bestaat), wat een functie is van een complexe variabele s. Het wordt meestal aangeduid met L f (t). De inverse Laplace-transformatie van een functie F(s) wordt beschouwd als de functie f (t) op zodanige wijze dat L f (t) = F(s), en in de gebruikelijke wiskundige notatie schrijven we, L ^-1F(s) = f (t).De inverse transformatie kan uniek worden gemaakt als null-functies niet zijn toegestaan. Men kan deze twee identificeren als lineaire operatoren die zijn gedefinieerd in de functieruimte, en het is ook gemakkelijk om dat te zien, L ^-1L f (t) = f (t), als null-functies niet zijn toegestaan.

De volgende tabel bevat de Laplace-transformaties van enkele van de meest voorkomende functies.

Wat is de Fourier-transformatie?

Gegeven een functie f (t) van een echte variabele t, zijn Laplace-transformatie wordt gedefinieerd door de integraal 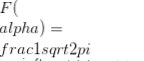(wanneer het bestaat), en wordt meestal aangeduid door F f (t). De inverse transformatie F ^-1F(α) wordt gegeven door de integraal . Fourier-transformatie is ook lineair en kan worden beschouwd als een operator die is gedefinieerd in de functieruimte.

Met behulp van de Fourier-transformatie kan de oorspronkelijke functie als volgt worden geschreven, op voorwaarde dat de functie slechts een eindig aantal discontinuïteiten heeft en absoluut integreerbaar is.

Wat is het verschil tussen de Laplace en de Fourier-transformaties?

• Fouriertransformatie van een functie f (t) is gedefinieerd als 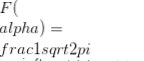, terwijl de laplace-transformatie ervan wordt gedefinieerd als zijnde .
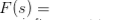• Fourier-transformatie wordt alleen gedefinieerd voor functies die zijn gedefinieerd voor alle reële getallen, terwijl voor Laplace-transformatie niet de functie hoeft te worden gedefinieerd die is gedefinieerd bij het instellen van de negatieve reële getallen.
• Fourier-transformatie is een speciaal geval van de Laplace-transformatie. Men ziet dat beide samenvallen voor niet-negatieve reële getallen. (d.w.z. neem s in de Laplace te zijn iα + β waar α en β zo echt zijn dat e ^β= ¹/_{√ (2ᴫ)})
• Elke functie die een Fourier-transformatie heeft, zal een Laplace-transformatie hebben, maar niet omgekeerd.