Verschil tussen reeks en reeks

In wiskunde en statistiek is de regel die reeks en reeks afbakent dun en wazig, waardoor velen denken dat deze termen één en hetzelfde zijn. Niettemin verschilt het begrip volgorde van series in de zin dat volgorde verwijst naar een rangschikking in de bepaalde volgorde waarin verwante termen elkaar opvolgen, d.w.z. het heeft een geïdentificeerde eerste eenheid, tweede eenheid, derde eenheid enzovoort.

Wanneer een reeks een bepaalde regel volgt, wordt deze als progressie genoemd. Het is niet precies hetzelfde als serie die wordt gedefinieerd als de sommatie van de elementen van een reeks. Lees het artikel om te weten wat het significante verschil is tussen reeks en reeks.

Inhoud: reeks Vs-serie

Vergelijkingstabel

Basis voor vergelijking	Volgorde	Serie
Betekenis	Sequentie wordt beschreven als de reeks getallen of objecten die een bepaald patroon volgt.	Serie verwijst naar de som van de elementen van de reeks.
Bestellen	Belangrijk	Soms belangrijk
Voorbeeld	1, 3, 5, 7, 9, 11 ... n ...	1 + 3 + 5 + 9 + 11 ... n ...

Definitie van sequentie

In de wiskunde een geordende set objecten of nummers, zoals een₁, een₂, een₃, een₄, een₅, een₆… een_{n ... .}er wordt gezegd dat ze in een reeks zijn, als, volgens bepaalde regels, een duidelijke waarde heeft. De leden van de reeks worden term of element genoemd die gelijk is aan elke waarde van het natuurlijke getal. Elke term in een reeks is gerelateerd aan de voorgaande en volgende term. Over het algemeen hebben reeksen verborgen regels of patronen, waardoor u de waarde van de volgende term kunt achterhalen.

De nde term is de functie van geheel getal n (positief), beschouwd als de algemene term van de reeks. Een reeks kan eindig of oneindig zijn.

Eindige sequentie: Een eindige reeks is er een die stopt aan het einde van de lijst met getallen a₁, een₂, een₃, een₄, een₅, een₆… een_n, wordt vertegenwoordigd door:
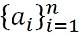
Oneindige sequentie: Een oneindige reeks verwijst naar een reeks die eindeloos is, een₁, een₂, een₃, een₄, een₅, een₆… een_{n ... .}., wordt vertegenwoordigd door:

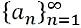
Definitie van serie

De toevoeging van de termen van een reeks (a_n), staat bekend als serie. Eenzelfde reeks kan ook eindig of oneindig zijn, waarbij een eindige reeks een reeks is met een eindig aantal termen geschreven als een₁+ een₂+ een₃ + een₄+ een₅ + een_{6 +}… een_n. In tegenstelling tot oneindige reeksen, waarbij het aantal elementen niet eindig of oneindig is, geschreven als een₁+ een₂+ een₃ + een₄+ een₅ + een_{6 +}… een_n+_{... .}

Als een₁+ een₂+ een₃ + een₄+ een₅ + een_{6 +}… een_n = S_n, dan S_n wordt beschouwd als de som tot n elementen van de serie. De som van termen wordt vaak weergegeven door Griekse letter sigma (Σ). Vandaar,

Belangrijkste verschillen tussen reeks en reeks

Het verschil tussen reeks en reeks kan duidelijk op de volgende gronden worden getrokken:

De reeks wordt gedefinieerd als de verzameling getallen of objecten die een bepaald patroon volgen. Wanneer de elementen van de reeks bij elkaar worden opgeteld, staan ze bekend als series.
Bestel zaken in een reeks, want er is een bepaalde regel die het patroon van de reeks voorschrijft. Vandaar dat 1, 2, 3 drie verschillend is van 3, 1, 2. Aan de andere kant, in een reeks lijkt het voorkomen of niet uit, zoals in het geval van absoluut convergerende reeksen, de volgorde er niet toe. Dus 1 + 2 + 3 is hetzelfde als 3 + 1 + 2, alleen de volgorde is anders.

Conclusie

Arithmetic Progression (A.P.) en Geometric Progression (G.P.) zijn ook reeksen, geen reeksen. Arithmetic Progression is een reeks waarin er een gemeenschappelijk verschil is tussen de opeenvolgende termen zoals 2, 4, 6, 8 enzovoort. Integendeel, in een meetkundig verloop is elk element van de reeks het gemene veelvoud van de voorgaande term zoals 3, 9, 27, 81 enzovoort. Evenzo is Fibonacci-reeks ook een van de populaire oneindige sequenties, waarin elke term wordt verkregen door de twee voorgaande termen 1, 1, 3, 5, 8, 13, 21 en zo verder op te tellen.

Opleiding