Hoe Halvering berekenen

In deze sectie zullen we leren over halfwaardetijd en de formule afleiden om de halveringstijd te berekenen. In radioactiviteit, halve leven is de tijd die de helft van de radioactieve kernen in een monster van een radioactieve isotoop nodig heeft om te vervallen. Het aantal radioactieve kernen in een monster vervalt exponentieel in de tijd. Om de halveringstijd te berekenen, wordt daarom de wiskunde van exponentieel verval gebruikt. Halfwaardetijd is een uiterst belangrijk concept voor toepassingen van radioactiviteit. Radio-isotopen die bijvoorbeeld in radiotherapie bij organen worden geïntroduceerd, mogen niet te lang in het lichaam van een patiënt blijven hangen. Aan de andere kant moeten isotopen die worden gebruikt voor het dateren van historische artefacten lange halfwaardetijden hebben, zodat genoeg van hen tot de dag van vandaag zijn gebleven om de leeftijd van de objecten te bepalen.

Verschil tussen willekeurige en spontane aard van radioactief verval

Radioactief verval is gecategoriseerd als beide willekeurig en spontaan.

• Radioactief verval is willekeurig omdat we niet kunnen bepalen wanneer een bepaalde kern zal vergaan, of bepalen hoe lang het zou duren voordat een bepaalde kern zou vergaan. Bijgevolg heeft elke radioactieve kern in een monster dezelfde kans om op een bepaald moment te vervallen.
• Radioactief verval is spontaan omdat het niet wordt beïnvloed door externe omstandigheden.

Wat is Half Life

Het aantal radioactieve kernen in een monster neemt af, omdat zodra de kern vervalt door alfa-, bèta- en gamma-verval, ze niet opnieuw hetzelfde vervalproces kunnen ondergaan. Het aantal radioactieve kernen in het monster neemt exponentieel af.

De activiteit, of de verval snelheid,is de mate van verandering van het aantal radioactieve kernen. Dit wordt gegeven door,

Het negatieve teken betekent dat het aantal radioactieve kernen in een steekproef is afnemende na een tijdje. $ latex \ lambda & s = 1 $ wordt het verval constant. Het geeft de kans dat een bepaalde kern per tijdseenheid vervalt. De vervalconstante heeft een specifieke waarde voor elk gegeven nucleair vervalproces. Hoe hoger de , hoe groter de kans op verval en het aantal radioactieve kernen in het monster neemt sneller af.

Als het aantal radioactieve kernen in een steekproef tegelijk is  is , dan het aantal radioactieve kernen in het monster na een tijdje  is gegeven door:

Het aantal radioactieve kernen in het monster neemt af exponentieel. Halve leven () Is de hoeveelheid tijd die nodig is om het aantal radioactieve kernen in de tijd te halveren. Als we een grafiek tekenen van hoe het aantal radioactieve kernen in de steekproef in de loop van de tijd varieert, krijgen we de volgende grafiek:

Hoe halveringstijd berekenen - Radioactieve vervalcurve

Hoe activiteit te berekenen

De activiteit van het monster is evenredig met het aantal aanwezige radioactieve kernen. Dus we kunnen een gelijkwaardige verklaring afleggen,

waar  is de activiteit van het monster op het moment , met  de activiteit wanneer .

Als een grafiek van activiteit versus tijd wordt getekend, zal deze een grafiek met dezelfde vorm produceren (dat wil zeggen activiteit neemt ook exponentieel af).

Activiteit wordt gemeten met de SI-eenheid becquerel (Bq). Een activiteit van 1 Bq komt overeen met een snelheid van 1 verval per seconde. De curie (Ci) is een andere eenheid die wordt gebruikt om activiteiten te meten. 1 Ci = 3,7 × 10¹⁰ bq.

Half Life Formula

We zullen nu een formule afleiden om de halveringstijd van het verval constant te krijgen. We beginnen met,

Na een tijdje , het aantal radioactieve kernenhelften. Zo, , of

Door de natuurlijke logaritme van beide kanten te nemen, krijgen we:

en dus, 

Hoe Halvering berekenen

voorbeeld 1

Indium-112 heeft een halfwaardetijd van 14,4 minuten. Een monster bevat 1,32 x 10²⁴ atomen van Indium-112.

a) Vind de vervalconstante

b) Ontdek hoeveel atomen van Indium-112 na 1 uur in het monster zouden achterblijven.

a) Sinds ,

b) Gebruik ,  atomen.

Voorbeeld 2

Tijdens een behandeling voor schildklierkanker krijgt een patiënt een monster van te innemen jodium-131, dat een activiteit van 1,10 MBq heeft. De halfwaardetijd van Jodium 131 is 8,02 dagen. Zoek de activiteit van jodium-131 ​​in het lichaam van de patiënt na 5 dagen na inname.

We gebruiken . Eerst werken we :

Dan,

MBq.

Notitie:

1. We berekenden direct de vervalconstante per dag en hielden de halfwaardetijd ook in dagen. Dus de dagen werden geannuleerd toen we berekenden 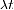 en het was niet nodig om tijden om te zetten naar seconden (dat zou ook goed hebben gewerkt, maar het zou iets meer zijn geweest)
2. In werkelijkheid zou de activiteit kleiner zijn. Dit komt omdat er ook een biologische halfwaardetijd geassocieerd is met de activiteit. Dit is de snelheid waarmee de patiënt radioactieve kernen uit hun lichaam afscheidt.

Voorbeeld 3

Bereken de halveringstijd van een radioactieve isotoop waarvan de activiteit in 1000 jaar met 4% afneemt.

4% = 0.04. We hebben nu 

.  Aan beide kanten,

per jaar.

216 jaar.